基本数据结构

本篇文章主要讲实现一些基本的数据结构，并且讲一些对其理解，以及最后怎么样用数组去实现这些数据结构。

链表

链表是使用指针实现的动态数据结构的最好和最简单的示例。对于链表来说，其对于数组(array)的优势在于：

  1. 我们可以在一个列表的中间增加或者移除数据
  2. 我们并不需要去预先定义这个列表的大小

同时，链表的缺点如下：

  1. random access是不可能的，我们需要从头开始遍历链表
  2. 我们需要动态分配以及使用指针，代码会变得复杂，可能会有内存泄漏以及segment fault
  3. 链表的开销(overhead)要比数组大，因为动态分配的缘故，在内存的高效使用上不如数组，并且每一个在这种类型的list里面的item都需要一个额外的pointer

我们重新回顾一下关于链表的细节：链表就是一个node的set，每一个node都有一个value以及一个指向下一个node的指针。如果某个pointer是null，那么这个node就是list的最后一个node。并且如果这个pointer是第一个node，那么这个list就是空的。

下面是基本的链表功能实现，需要注意的如下：

  1. 涉及对指针操作，比如删除头节点或者删除中间节点（特殊情况就是删除头节点）的时候，我们需要对指针操作，由于函数的性质，这里需要传入的是pointer to pointer，这样我们可以修改指针的值；
  2. 我们把这种node结构体中的指针next称为一种递归的manner，把node_t称为node type，这样子在我们定义的时候，我们可以直接使用node_t，而不用去写struct node；
  3. 实际上对于函数来说，修改的都是副本，但是为什么可以直接对next做指向修改？因为这里传入的也是指针的指针。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
#include <stdlib.h>
#include <stdio.h>

typedef struct node{
    int val;
    struct node* next;
}node_t;

void print_list(node_t *head){
    node_t * current = head;

    while(current != NULL){
        printf("%d\n", current->val);
        current = current->next;
    }
}

// 向链表的最后加入元素
void push(node_t* head, int val){
    node_t *current = head;
    while(current->next != NULL){
        current = current->next;
    }

    current->next = (node_t *)malloc(sizeof(node_t));
    current->next->val = val;
    current->next->next = NULL;

}

// 对于链表的最好的use case是队列和栈
// 向链表的最头加入元素
void push_back(node_t ** head, int val){
    // 由于是在链表的头部插入指针，意思是头部指针的指向会发生改变，要在函数中改变指针的指向，就要传入pointer to pointer
    node_t * new_node;
    new_node = (node_t *)malloc(sizeof(node_t));

    new_node->val = val;
    new_node->next = *head;
    *head = new_node;
}

// 去除第一个元素
// 想要去除第一个元素，就是上一个操作的逆向操作
int pop(node_t **head){
    int retval = -1;
    node_t * next_node = NULL;

    if(*head == NULL){
        return -1;
    }

    next_node = (*head)->next;
    retval = (*head)->val;
    free(*head);
    *head = next_node;

    return retval;
}

int remove_last(node_t *head){
    int retval = 0;
    // 如果这里只有一个元素，那么直接去除
    if(head->next == NULL){
        retval = head->val;
        free(head);
        return retval;
    }

    //一般情况下，我就要得到倒数第二个元素
    node_t *current = head;
    while(current->next->next == NULL){
        current = current->next;
    }

    retval = current->next->val;
    free(current->next);
    current->next = NULL;
    return  retval;
}

// remove a specific item

// 1.Iterate to the node before the node we wish to delete
// 2.Save the node we wish to delete in a temporary pointer
// 3.Set the previous node's next pointer to point to the node after the node we wish to delete
// 4.Delete the node using the temporary pointer
int remove_by_index(node_t** head, int n){
    int i=0;
    int retval = -1;
    node_t* current = *head;
    node_t* temp_pop = NULL;

    if(n==0){
        return pop(head); // 涉及到对于head指针的操作，在这种情况下最好是传入pointer to pointer
    }

    for(i=0; i<n-1; i++){
        if(current->next ==NULL){
            return -1;
        }
        current = current->next;
    }

    if(current->next==NULL){
        return -1;
    }

    temp_pop = current->next;
    current->next = temp_pop->next;
    retval = temp_pop->val;
    free(temp_pop);

    return retval;
}

// exercise: You must implement the function remove_by_value which receives a double pointer to the head and removes the first item in the list which has the value val.
int remove_by_value(node_t** head, int val){
    int retval = -1;
    node_t * current = *head;
    node_t * front_node = NULL;

    if(*head==NULL){
        return -1;
    }

    if(current->val == val){
        retval = val;
        pop(head);
        return retval;
    }

    while(current->val != val){
        if(current->next == NULL){
            return -1;
        }
        front_node = current;
        current = current->next;
    }

    front_node->next = current->next;
    retval = current->val;
    free(current);

    return retval;
}

int main(){
    node_t* head = NULL;
    head = (node_t *) malloc(sizeof(node_t));

    if(head == NULL){
        return 1;
    }

    head->val = 1;
    head->next = NULL;
    printf("hello world\n");
}

——><参考于https://www.learn-c.org/en/Linked_lists>

链表的数组实现：

我们在日常学习的过程中，老师教授给我们的都是以结构体的形式实现的链表，但是呢，比如我们要创建100000个结点，这样的话， 用结构体的话，时间太长，空间太大，反观数组，就显得很有优势

1.数组的优缺点

认识数组：

数组是一种线性结构，存储的空间是内存连续的（物理连续），每当创建一个数组的时候，就必须先申请好一段指定大小的空间。（一次申请即可指定大小的空间）

*优点：*

由于内存连续这一特征，数组的访问速度很快，直到索引下标之后，可以实现O(1)的时间复杂度的访问。

缺点：

1.在任意位置删除和插入操作的时候，就会涉及到部分元素的移动，这样的话我们对于数组的任意位置的删除和插入的操作的时间复杂度为O(n)。

比如：

1>在i点后面插入数据，那么就需要i+1位置以及之后的元素，整体后移一位（for循环操作），然后再将插入的数据放在i+1的位置上

2>在i点之后删除元素，那么就需要，将i+1以及之后的元素，整体前移一位，总元素个数减一

以上是数组的优缺点，可以快速访问，达到O(1)，但是在任意删除和插入元素的时候，会耗时间，达到O(n)。

2.链表的优缺点

*认识链表*

1.链表也是一种线性结构，但是他存储空间是不连续的（物理不连续，逻辑连续），链表的长度是不确定且支持动态扩展的。每次插入元素的时候，都需要进行申请新节点，然后赋值，插入链表中。

优点：

在插入数据或者删除数据的时候，只需要改变指针的指向即可，不需要类似于数组那样部分整体移动，整个过程不涉及元素的迁移，因此链表的插入和删除操作，时间复杂度为O(1)

缺点：

在查找任意位置的结点的数值域的时候，需要遍历，时间复杂度为O(n)

但是我们在任意位置插入或者删除元素的时候，需要查找这个指定的元素的结点位置，所以综合起来，链表的插入和删除仍为O(n)。

3.总结

无论数组还是链表，查找的时间复杂度都是O(n)，查找都要挨个遍历，直到找到满足的条件的数据为止，所以对于链表，如果没有给定，指针的地址，只是要插入删除第N位元素的时候，加上查找，综合起来时间复杂度为O(n)。

但是我们如果以数组的形式来实现链表，那么插入删除指定元素位置的时候，是不是就更加简便了呢，在第N位插入删除元素的时候，直接以O(1)的时间复杂度找到该位置结点，然后再由于链表的删除插入都是O(1)的，所以整个删除或插入操作，综合时间复杂度为O(1),比普通链表快很多。（注意这里指定第N个位置的元素，是真的第N个，但是如果要找匹配的元素，仍然是O(N)的复杂度）

4.实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
#include <stdlib.h>
#include <stdio.h>

#define MAX_SIZE 10

// 数组模拟链表
int values[MAX_SIZE];       // 存储值的
int next[MAX_SIZE];         // 用于存储下一个节点的索引
int head = -1;              // 链表头部的索引，-1表示空链表
int free_index = 0;         // 下一个可用的空闲索引

void init(){
    for(int i=0;i<MAX_SIZE-1;i++){
        next[i] = i+1;      // 每个位置的“下一个”就是下一个可用的空闲空间（初始化的时候）,也有人直接写下一个空闲位置为 free_index ++
    }
    next[MAX_SIZE-1] = -1;  // 最后一个元素并没有下一个节点
    free_index = 0;         // 初始第一个空闲位置为0
}

void add(int value){
    if(free_index == -1){
        printf("链表已满，无法插入\n");
        return;
    }

    int new_node = free_index;      //获取空闲位置
    free_index = next[free_index];  //更新

    values[new_node] = value;
    next[new_node] = head;

    head = new_node;
}

// 从链表里面删除一个值为 value 的第一个节点
void remove_by_value(int value){
    if(head == -1){
        printf("链表为空\n");
        return;
    }

    int current = head;
    int prev = -1;

    while(current != -1 && values[current] != value){ // 这里current 为-1表示这里走到头了，因为最后一个元素的next的值为-1
        prev = current;
        current = next[current];
    }

    if(current == -1){
        printf("链表中未找到值为 %d 的节点\n", value);
        return;       
    }

    // 如果删除的是头节点
    if(prev == -1){
        head = next[head];
    }
    else{
        next[prev] = next[current];
    }

    //删除完要更新 free_index,这里核心宗旨是不改变next[free_index]，而改变free_index之前的指向，
    //也就是把current 当成当前的空闲，并且当前空闲的下一个空闲就是 free_index，最后更新 free_index为current
    next[current] = free_index;
    free_index = current;
}

void print_list(){
    int current = head;
    printf("链表: ");
    while(current != -1){
        printf("%d ->", values[current]);
        current = next[current];
    }
    printf("NULL\n");
}

int main(){
    init();

    add(10);
    add(20);
    add(30);
    print_list();

    remove_by_value(10);
    print_list();

    remove_by_value(20);
    print_list();

    remove_by_value(30);
    print_list();

    return 0;

}

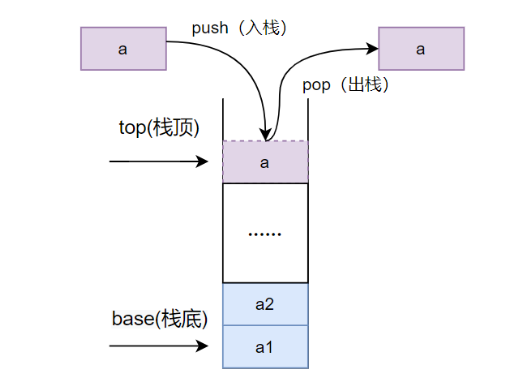
链栈

栈是一种后进先出的数据结构，我们可以用链表来实现栈，这样的话，我们可以在栈的顶部插入和删除元素，这样的话，我们可以在O(1)的时间复杂度内完成这个操作。栈的实现方式有很多，比如数组，链表，这里首先介绍链表的实现方式。

image-20240926201907962

单链表可以在表头、表尾或者其他任意合法位置插入元素，如果只能在单链表的表尾插入和删除元素，那么就可以将其视为链栈。
因此，在单链表的基础上，我们再维护一个top指针即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <stdlib.h>
#include <stdio.h>

// 链栈节点
typedef struct stack_node{
    struct stack_node * next;
    void *data;
}stack_node;

// 链栈体, top指向的栈节点的结构体，栈结构体还包括一个长度信息
typedef struct stack{
    struct stack_node* top;
    int length;
}stack;

// 栈函数体清单
// stack_create         O(1)
// stack_release        O(N)
// stack_push           O(1)
// stack_pop            O(1)
// stack_empty          O(N)

stack* stack_create(){
    stack* stack = (struct stack*)malloc(sizeof(struct stack));
    if(stack == NULL) return NULL;

    stack->length = 0;
    stack->top = NULL;

    return stack;
}

stack* stack_push(stack* stack, void * data){
    stack_node *node = (stack_node*)malloc(sizeof(stack_node));
    if(node == NULL){
        return NULL;
    }

    node->data = data;

    // 插入
    node->next = stack->top;
    stack->top = node;

    stack->length++;
    return stack;
}

void* stack_pop(stack* stack){
    // 出栈时，首先临时保存栈顶节点指针，用于在返回栈顶节点数据域的值之前的释放操作
    stack_node *curr = stack->top;
    if(curr == NULL){
        return NULL;
    }

    void *data = curr->data;
    stack->top = stack->top->next;

    free(curr);
    stack->length--;
    return data;
}

// 清空栈中的所有元素，但是不删除栈
void stack_empty(stack* stack){
    int length = stack->length;
    stack_node *curr, *next;
    curr = stack->top;

    while(length--){
        next = curr->next;
        free(curr);
        curr = next;
    }

    stack->length = 0;
    stack->top = NULL;

    // while(stack->length--){
    //     stack_pop(stack);
    // }
    // stack->top = NULL;
    // 也可以换成注释这块，但是效率会大大降低，因为每次进函数都会压栈什么的，并且会有很多额外的开销，比如更新stack的状态信息，这两种代码编写在编译运行的时候就能看出来很大的差别
}

void stack_release(stack *stack){
    stack_empty(stack);
    free(stack);
}

int main()
{
    char a = 'a';
    char b = 'b';
    char c = 'c';

    /* 创建一个栈 */
    stack *stack = stack_create();

    printf("%p\n", stack_pop(stack)); // %p 会输出指针的值，通常是一块内存地址，如果是空那么就输出nil或者0x0，取决于编译平台

    /* 压栈 */
    stack_push(stack, &a);
    stack_push(stack, &b);
    stack_push(stack, &c);
    /* 出栈 */
    while (stack->length > 0)
    {
        printf("%c\n", *(char *)stack_pop(stack));
    }

    /* 压栈 */
    stack_push(stack, &a);
    stack_empty(stack);
    printf("%p\n", stack_pop(stack));

    /* 释放栈 */
    stack_release(stack);
    return 0;
}

栈的数组实现

栈的数组实现比较简单，这里只需要注意show的时候，从top开始递减print就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <stdio.h>
#include <stdlib.h>

#define SIZE 4

int top = -1, inp_array[SIZE];
void push();
void pop();
void show();

int main()
{
    int choice;

    while (1)
    {
        printf("\nPerform operations on the stack:");
        printf("\n1.Push the element\n2.Pop the element\n3.Show\n4.End");
        printf("\n\nEnter the choice: ");
        scanf("%d", &choice);

        switch (choice)
        {
        case 1:
            push();
            break;
        case 2:
            pop();
            break;
        case 3:
            show();
            break;
        case 4:
            exit(0);

        default:
            printf("\nInvalid choice!!");
        }
    }
}
// push检查溢出情况
void push(){
    int x;

    if(top == SIZE-1){
        printf("\nOverflow!");
    }
    else{
        printf("\nEnter the element to be added to the stack:");
        scanf("%d", &x);

        top = top + 1;
        inp_array[top] = x;
    }
}

// pop 检查向下溢出
void pop()
{
    if (top == -1)
    {
        printf("\nUnderflow!!");
    }
    else
    {
        printf("\nPopped element: %d", inp_array[top]);
        top = top - 1;
    }
}

void show(){
    if(top == -1){
        printf("\nUnderflow!!");
    }
    else{
        printf("\nElements present in the stack: \n");
        for (int i = top; i >= 0; --i)
            printf("%d\n", inp_array[i]);
    }
}

队列

队列是一种先进先出的结构，是一种线性的表。队列的表示也有顺序和链式两种，这里我们先介绍链式队列的实现。

我们可以将链式队列理解成为一种特殊的链表，只允许在表头删除，在表尾进行插入操作。因此，在定义队列结构体的时候，我们需要去维护一个头指针和一个尾指针。

下面是对应队列函数的清单：

函数 作用 算法复杂度
queue_create 创建新队列 O(1)
queue_release 释放队列，以及队列中的节点 O(N)
queue_push_data 入队 O(1)
queue_pull_data 出队 O(1)
queue_empty 释放队列中节点(头节点除外)，但不释放队列本身 O(N) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include <stdio.h>
#include <stdlib.h>

typedef struct queue_node{
    struct queue_node* next;
    void *data;
}queue_node;

// 同理，继续定义队列本身
typedef struct queue{
    struct queue_node *head;
    struct queue_node *tail;
    int length;
}queue;

queue *queue_create(){
    queue *queue = (struct queue*)malloc(sizeof(struct queue));

    // 为了方便操作，这里为队列创建一个队列节点，并且头尾都指向这里
    queue_node *node = (struct queue_node*)malloc(sizeof(struct queue_node));

    if(queue == NULL || node == NULL) return NULL;

    node->data = NULL;
    node->next = NULL;

    // 对队列进行初始化
    queue->head = node;
    queue->tail = node;
    queue->length = 0;

    return queue;
}

// 有元素入队，那么就是对尾指针操作
queue *queue_push_data(queue *queue, void *data){
    queue_node *node = (queue_node*)malloc(sizeof(queue_node));

    if(node == NULL) return NULL;
    node->data = data;

    queue->tail->next = node;
    queue->tail = queue->tail->next;
    queue->length++;
    return queue;
}

// 对于出队列，就是维护一个头指针
void *queue_pull_data(queue *queue){
    // 构建一个临时的指针保存当前头指针的节点
    queue_node *curr = queue->head->next;

    // 默认节点的下一个节点才是真正的数据节点，因为我们是按照定义来的，默认创建就是length=0并且有一个节点，那么就应该是找 head->next
    if(curr == NULL) return NULL;

    void*data = curr->data;

    queue->head->next = curr->next;
    // 判断这个队列里面是否是除了初始节点之外，只有一个节点，如果是这样的话，我们要避免pop的时候尾指针的丢失
    if(queue->tail == curr){
        queue->tail = queue->head;
    }

    free(curr);
    queue->length--;
    return data;
}

void queue_empty(queue *queue){
    int length = queue->length;
    queue_node *curr = queue->head->next;
    queue_node *next;
    
    while(length--){
        next = curr->next;
        free(curr);
        curr = next;
    }

    queue->head->next = NULL;
    queue->head->data = NULL;
    queue->tail = queue->head;
    // 保证指针不悬空

    queue->length = 0; 
}

void queue_release(queue *queue){
    // 释放元素
    queue_empty(queue);

    free(queue->head);
    free(queue);
}

// 测试代码
int main(){
    char a = 'a';
    char b = 'b';
    char c = 'c';

    queue *queue = queue_create();
    printf("%p\n", queue_pull_data(queue));

    queue_push_data(queue, &a);
    queue_push_data(queue, &b);
    queue_push_data(queue, &c);

    while(queue->length){
        printf("%c\n", *(char *)queue_pull_data(queue));
    }
    
    queue_push_data(queue, &c);
    queue_push_data(queue, &c);

    /* 释放队列中的节点 */
    queue_empty(queue);
    printf("%p\n", queue_pull_data(queue));

    /* 释放队列 */
    queue_release(queue);
    return 0;
}

顺序队列

用数组模拟队列主要要注意以下几点：

  1. MAX_SIZE 为该队列的最大元素数目
  2. rear指向队列的最后元素
  3. front指向队列最前元素的前一个
  4. 队列是空的条件为：front == rear
  5. 队列是满的条件为：rear == MAX_SIZE - 1

顺序队列的“假溢出”问题

顺序队列因多次入队列和出队列操作后出现的尚有存储空间但不能进行入队列操作的溢出称作假溢出。简单地说，就是**顺序队列只能使用一次，没有达到复用的效果。**可以改进成顺序环形队列避免这个问题，循环顺序队列后面会讲。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
#include <stdlib.h>
#include <stdio.h>

#define MAX_SIZE 5

typedef struct{
    int queue[MAX_SIZE];
    int rear;
    int front;
}ArrayQueue;

void QueueInitialize(ArrayQueue *Q){
    memset(Q, 0x00, sizeof(Q->queue));
    Q->front = -1; // 初始化队头，指向队列头的前一个位置
    Q->rear  = -1; // 初始化队尾，指向队尾,指向具体的数据
}

// 判断队列满
int isFull(ArrayQueue Q){
    if(Q.rear == MAX_SIZE - 1){
        return 1; // 队列满返回1
    }
    else{
        return 0;
    }
}

int isEmpty(ArrayQueue Q){
    if(Q.front == Q.rear){
        return 1;
    }
    else{
        return 0;
    }
}

int addQueue(ArrayQueue *Q, int n){
    if(Q->rear == MAX_SIZE - 1){
        printf("队列已满无法添加数据\n");
        return 0;
    }

    Q->rear++;
    Q->queue[Q->rear] = n;
    return 1;
}

// 这里设计返回两个，一个是操作状态，一个是数据，所以要传一个指针进去，带回到main函数
int getQueue(ArrayQueue *Q, int *d){
    if(Q->front == Q->rear){
        printf("队列为空无法获取数据\n");
        return 0;
    }
	
	Q->front++; 
    *d = Q->queue[Q->front];
    Q->queue[Q->front] = 0; // 取出后赋值为0

    return 1;
}

void showQueue(ArrayQueue Q){
    int i;
    if(isEmpty(Q)){
        printf("队列为空，没有数据\n");
    }
    else{
        for(i=Q.front+1; i<=Q.rear; i++){
            printf("%d\n",Q.queue[i]);
        }
    }
}

// 显示队头数据，而不是取出数据

//显示对头数据， 注意不是取出
int headQueue(ArrayQueue Q, int *d){
	//判断是否为空 
	if(isEmpty(Q)){
		printf("队列为空，无对头数据可显示\n");
		return 0;
	}
	*d = Q.queue[Q.front + 1];
	return 1;
} 


int main(int argc, char *argv[]) {
	//测试数据
	ArrayQueue Q;
	int loop = 1, value, res;
	char key; 
	
	//初始化队列
	QueueInitialize(&Q);
	
	while(loop) {
		printf("s(show): 显示队列\n");
		printf("e(exit): 退出程序\n");
		printf("a(add): 添加数据到队列\n");
		printf("g(get): 从队列里面取数据\n");
		printf("h(head): 查看队列头的数据\n");
		key = getchar();
		switch(key){
			case 's':  //显示队列 
				showQueue(Q);
				break;
			case 'a':  // 添加数据到队列
				scanf("%d", &value);
				addQueue(&Q, value);
				break;
			case 'g': //从队列里面取数据
				if(getQueue(&Q, &res)){
					printf("取出的数据是：%d\n", res);
				}
				break;
			case 'h':  //查看队列头的数据
				if(headQueue(Q, &res)){
					printf("当前对列头的数据是：%d\n", res);
				}
				break;
			case 'e':
				loop = 0;
				break;
			default:
				break;
		}
		getchar();  //吸收回车，避免前面的目录两次输出 
	}
	printf("程序退出\n");
	return 0;
}