性能优化学习笔记8
多线程算法分析
这一章节的内容主要是关于对分支递归的并行性分析 🥵
算法回顾,分治递归的并行性

首先我们来看递归树,可以知道深度为,并且我们可以计算出来每一层的时间复杂度为,所以我们可以得到总的时间复杂度为。上述,其中是子问题的个数,是每个子问题的规模,是合并子问题的时间复杂度。并且与$ a^{\log_{b}n} $是等价的,只需要对两个式子取对数即可得到(取log以b为底的对数)。
现在有一个问题:这些级别的工作量是多少?——我们要比较与的大小:

上述符号中,Big O符号表示的是一个上界,Big 符号表示的是一个下界,Big 符号表示的是一个确切的界。我们可以看到,如果与相比,的增长速度更快,那么我们就可以认为是主导的,反之,是主导的。同时,当与相等时,该工作量为,注意,这里的K是要大于等于0的。
以下是一个应用上述公式的例子:

如图所示,这里的第二个式子,k=0,符合要求,而对于第四个式子,这里的,k=-1,不符合要求。
Cilk loop parallelism
外层循环cilk
上节课关于矩阵的转置代码,我们都知道,可以通过cilk_for来实现并行性,具体cilk是怎么实现再循环中并行呢?实际上还是用的分治递归的思想:

我们可以看到,如果仅仅针对外层循环做cilk操作,那么实际上就是对i做了一个分治递归,那么我们可以绘制出这样的DAG图像:
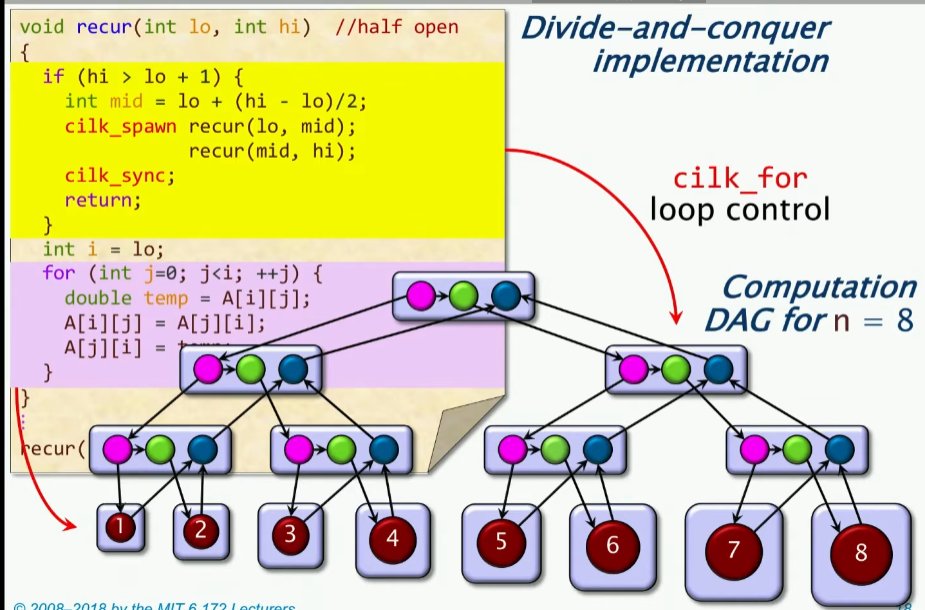
现在问题来了,上一节课我们学习到了如何进行计算并行度,主要是两个公式:Work和Span。只不过这里不再是具体的数字,而是一个Big O符号。
上述图中的相关量计算如下:
- Work: (很明显,双重循环)
- Span: (这里关于循环控制的span是lgn,但是关于最大的span还是n,因为这里我只是把外层循环进行了分治,所以内部要走的最长路径仍然是n,因此关于这条最长的路径,一去一回,去是N,回来是lgn)
- Parallelism: (这里的Parallelism是Work/Span,也就是说,这里的并行度是n)
双层循环cilk
如果我们对双层循环都进行cilk操作,那么现在,我们的work和span是多少呢?
其实很简单,我们可以看到,我们的work是不变的,即,而对于span,已经发生了改变,外层循环控制是lgn,内层循环也变成了lgn,最内层叶子节点的操作变成了,所以我们可以得到,那么我们可以得到并行度为。

多层循环cilk的问题
如果你的并行度要远大于处理器的数量,那么这样的方法很好,也就是说,如果对于上面我们只是用外层cilk,得到的并行度n要远远大于处理器的数量的话,实际上我们并不需要对内层循环进行cilk操作,因为这样的话,我们会浪费很多的资源,因为我们的并行度已经很大了。
现在有一个问题,上述双层循环都是用cilk操作,在实践中,它是更好的算法吗?我们来考虑向量加法。
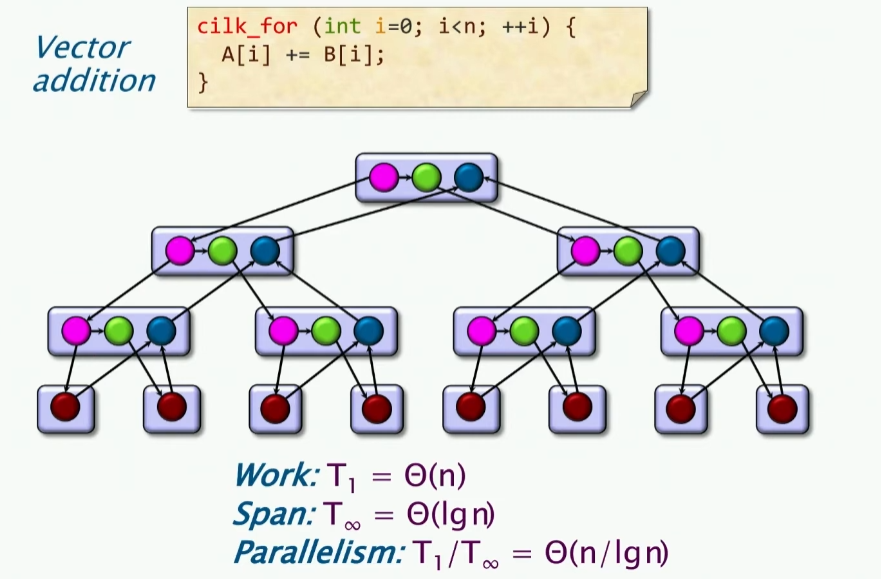
实际上,如果我们进行并行计算的话,会带来额外的开销,我们具体阐述如下:
(上述开销包括内存访问存取、子例程调用等等)

因此我们对其进行了改进,加入了一个阈值。我们考虑在阈值情况下的并行度:
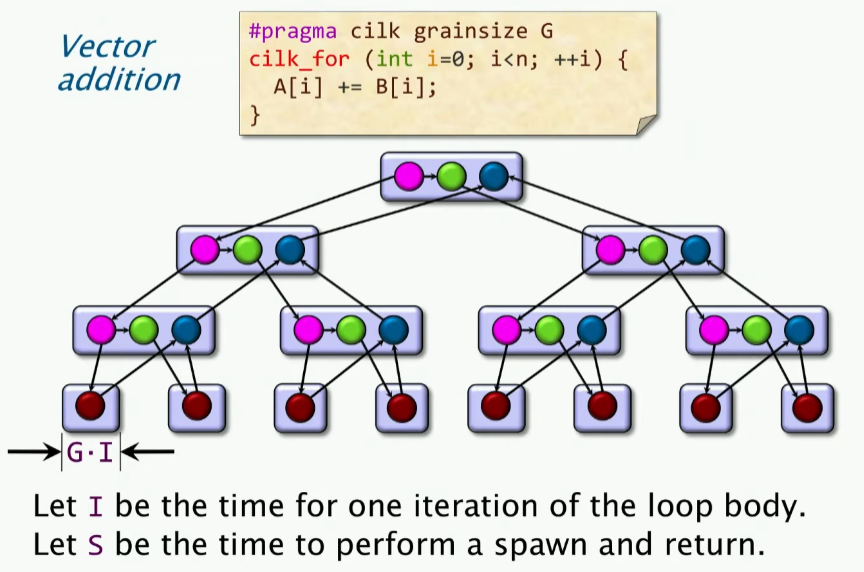
上述S即执行生成和返回的时间,我们重新计算并行度:
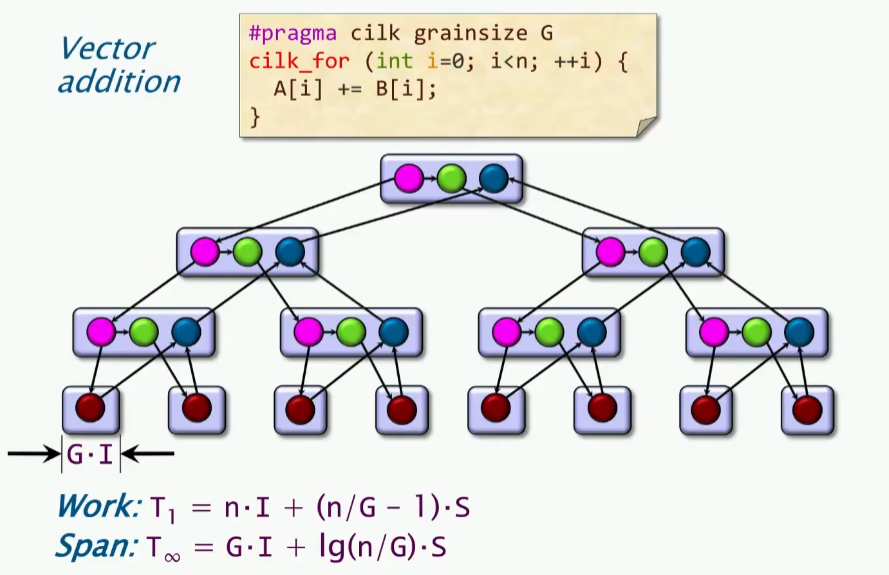
我们可以知道,其中n/G是叶子节点的数量,所以n/G-1就是非叶子节点的数量,而其中的log(n/G),就是循环控制的深度。
我们发现一个有意思的现象就是,我们想要work小(肯定是减少开销而不是增大开销),那么就是G要变大,但是我们想要span也变小,那么G要变小,这就是一个矛盾的地方。因此,我们得到的结论就是:

另一种向量并行加法
这里有一个实现方法,就是不在简单的外层循环的角度去做并行:

我们以G作为单位进行分拆。也就是说,以G为一个step,进行分拆,我们绘制DAG图:
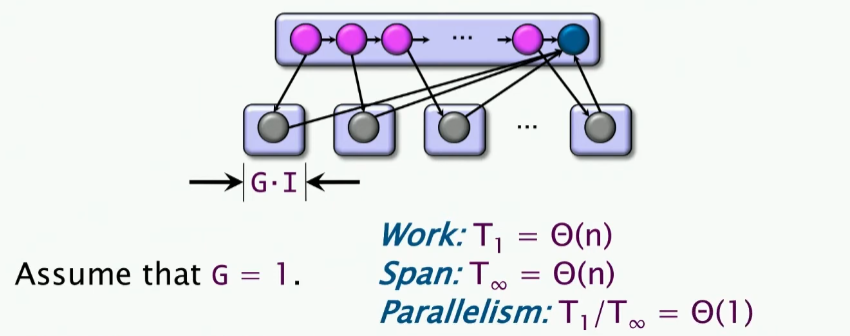
但是很让人伤心的是,这样的并行度是微不足道的,即PUNY 😟 😟 😟。现在我们增大G,再来看看并行度如何:
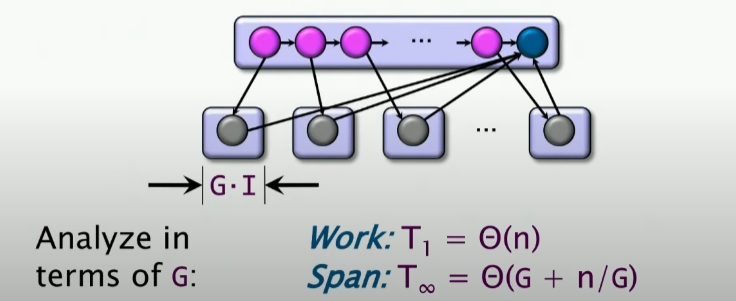
以后看到这种问题,基本上求span就是循环控制的span+叶子节点的span。 🤓 🤓
因此,我们从数学角度去看,如何获得最小的span呢?即最大的并行度呢?我们可以得到一个结论:

一些总结
- 当我们通过最小化span去最大化并行度的时候,最好得到的并行度要比处理器数量多10倍多,这样以达到了最接近线性加速的效果;
- 当我们得到了足够多的并行度的时候,尝试去做更多的trade-off去减少额外的开销,即work overhead;
- 使用分治递归或者并行循环,但是不要在一个很小的事情中做并行,这样带来的开销反而会更大;
- 确保每一次做并行的工作量都是足够大的,这样才能够达到最大的并行度;
- 可以使用函数内联或者函数调用来粗化粒度,这样可以减少开销。
- 如果你被迫做出选择,要选择在外部循环做并行,而不是在内部,因为内部往往涉及资源竞争;
矩阵乘法
我们在早些的课程中得知,矩阵乘法涉及三层loop:
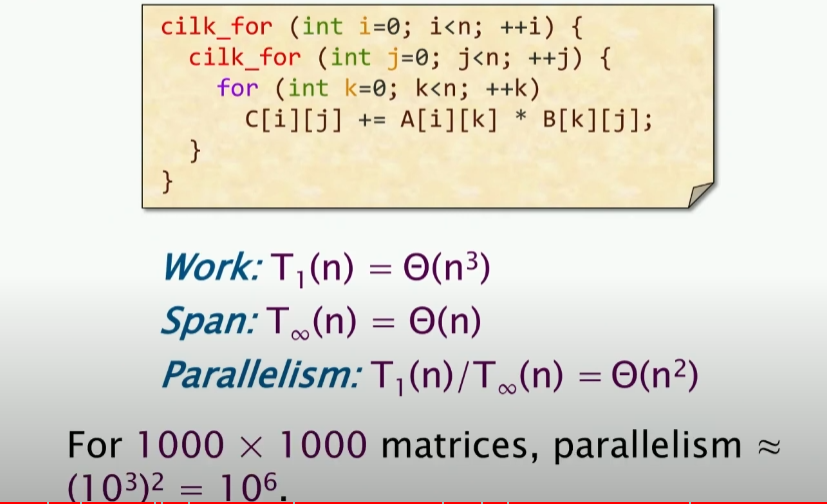
我们对外部两层做并行,得到的并行度是,span是两个logn加上n,所以我们得到的并行度是。
更有效地使用cache
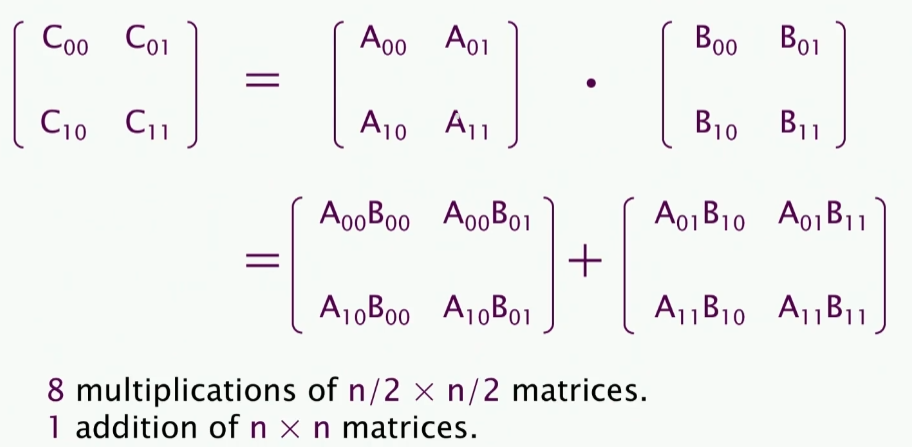
上述矩阵乘法,可以拆分成上述形式,这实际上是Strassen算法的思想。(拆分成八乘法以及一次加法)
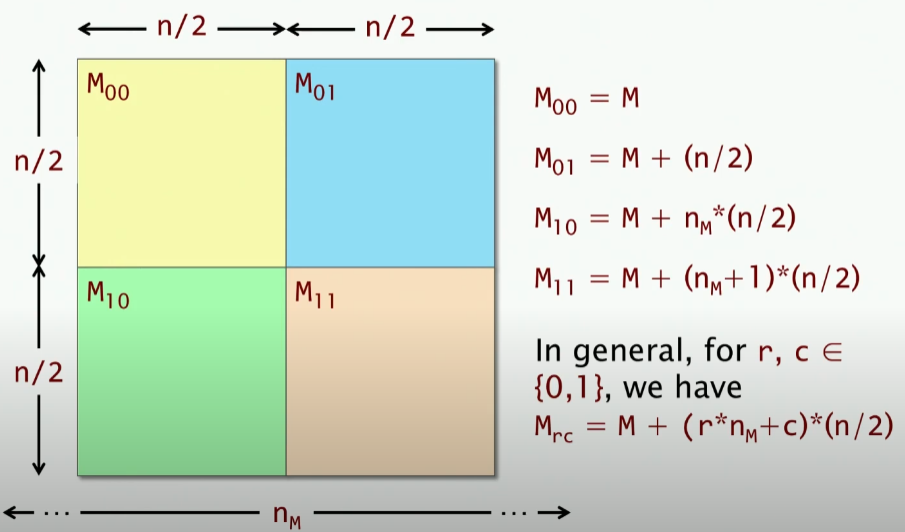
一个矩阵,我们可以分成四个部分,这里的M代表Memroy,实际上寻址可以看成是以行为优先级的顺序存储,实际上是一个一元的数组,那么我们就很好理解这里的寻址了,其中代表行的长度,因此我们得到上述每个子矩阵的左上角开始位置,并且得到了上述通用的任意位置的矩阵的寻址方法。
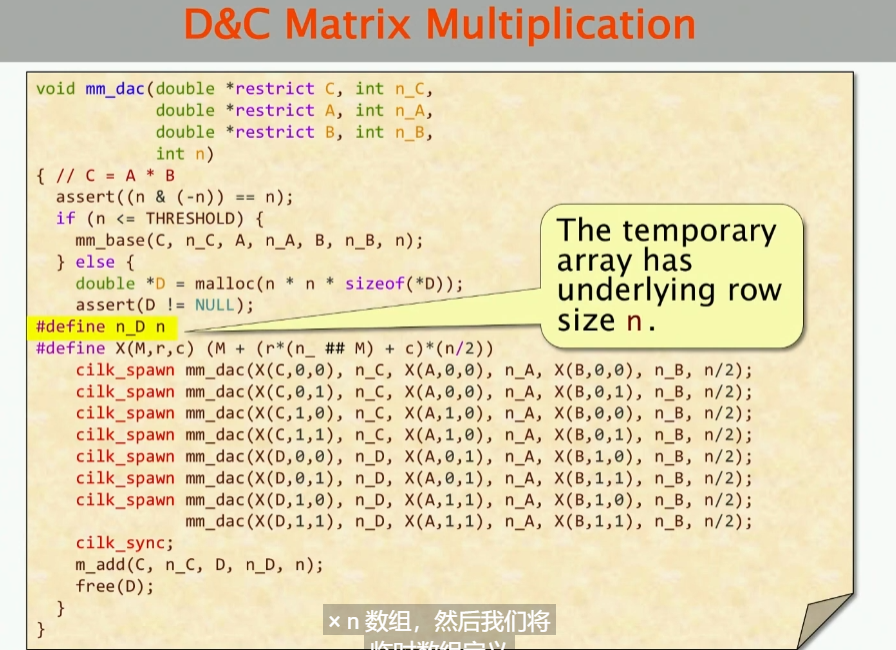
这里实际上,就是代码实现,做cilk_spawn然后最后求和,这里也有一些细节,比如上述assert方法是一个很快的实现判断这个数是否是2的次幂的bit tricks。


