竞争与并行性

上一节我们对于cilk有一个认识，就是Cilk keywords 是授予并行执行的权限，它们并不要求并行执行。编译器可以选择不并行执行，而是按照顺序执行。这种选择是为了提高性能，因为并行执行有时候会带来额外的开销。在这一节中，我们将讨论一些并行执行的问题，包拋竞争和死锁。（就像爱情一样，强扭的瓜不甜，两个人最好是都有各自奋斗的目标 😎 ）

Determinacy Races 确定性竞争

定义：两个逻辑上并行的指令访问同一个内存位置，并且至少有一个是写操作。

我们用一个cilk_for 引入确定性竞争：

1
2
3
4
5
int x = 0;
cilk_for (int i = 0; i < 100; i++) {
    x++;
}
assert(x == 2);
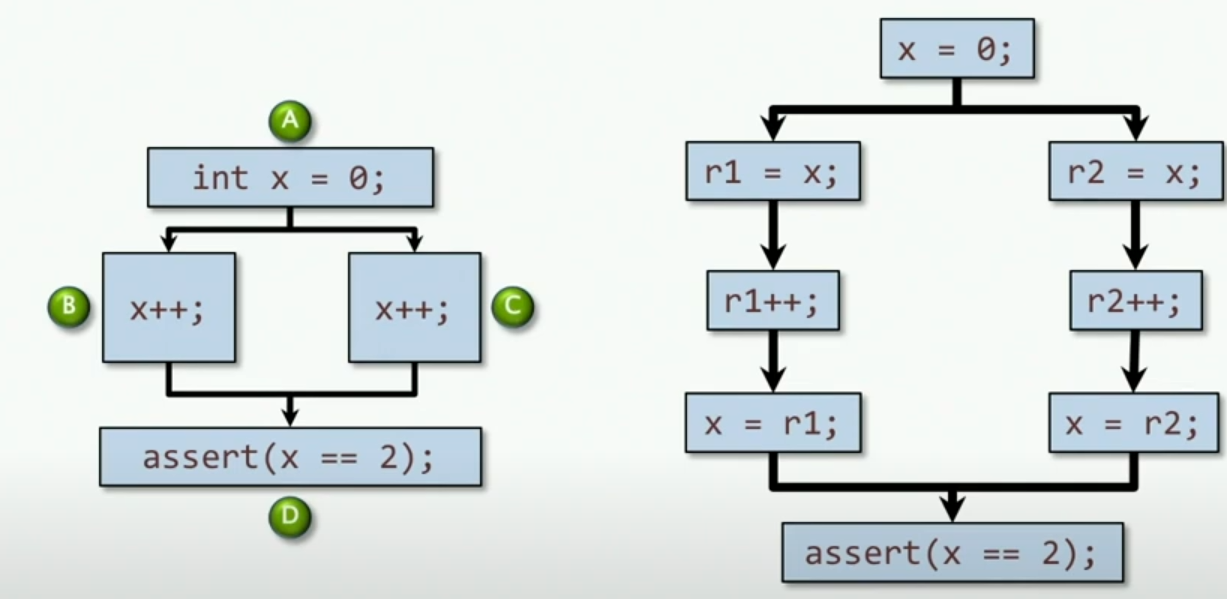
image-20240521154302852

实际上，上述代码我们可以得到这样的图片，并且实际上执行increment操作是需要三步骤的，通过寄存器实现。因此，这样就会出现竞争，出现不同寄存器都要写入同一个位置的情况。那么对于执行的结果而言，不一定每次都是错误的，比如说我左边的那条路先跑完，然后再跑右边的路，这样就与顺序执行结果相同。

这样的竞争有两种：

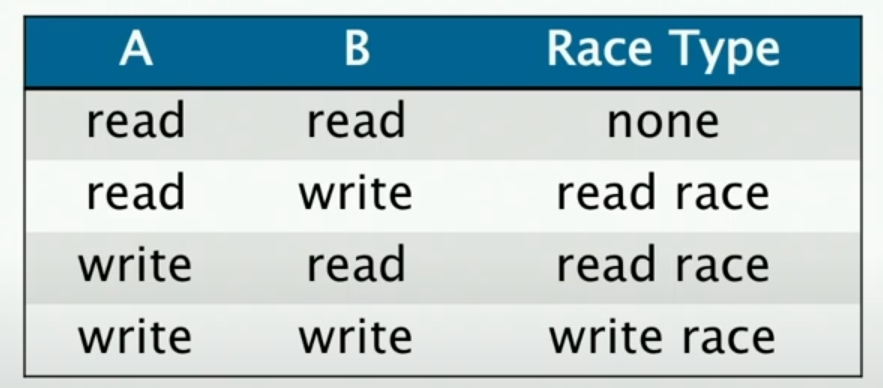
image-20240521154846470
  • 读竞争，我们不知道读的结果是不是正确的
  • 写竞争，同理

我们定义两段代码是独立的，当且仅当它们之间没有确定性竞争。这样的定义是为了保证程序的正确性，因为我们不知道这样的竞争会不会导致错误的结果。

Avoiding Races

  • cilk_for 中的迭代应该是独立的
  • 在cilk_spawn 与 cilk_sync之间的子级代码应该要独立于父级代码，这也包括由生成的子级代码调用的子级执行代码
  • 机器字的大小很重要！小心在packed data structures中的竞争
    image-20240521155440858
    对于我们的英特尔机器，如果我们使用基本的数据类型比如字符、整型等等并不会出现竞争，但是如果使用非标准的类型——如果我们使用C的bit fields，并且该字段并不是标准大小之一，那么就可能遇到竞争

Cilksan Race Detector

我们可以通过 -fsanitize=cilksan 来检测竞争，这样可以启动cilk的竞争检测器，根据给定的输入检测并行情况下的结果与顺序执行的结果是否一致。并且给出可能存在竞争的内存位置，其根据程序员的输入来判断是否是竞争，报告这些竞争。

什么是并行性

现在我们重新审视一下并行性，我们还是从斐波那契数列例子开始：

1
2
3
4
5
6
7
8
9
10
11
// cilk code for Fibonacci
int64_t fib(int n) {
    if (n <= 1) {
        return n;
    } else {
        int64_t x = cilk_spawn fib(n-1);
        int64_t y = fib(n-2);
        cilk_sync;
        return x + y;
    }
}

上述为clik的斐波那契数列代码实现，这里对不同的代码进行颜色编码，给出具体的执行流程图：

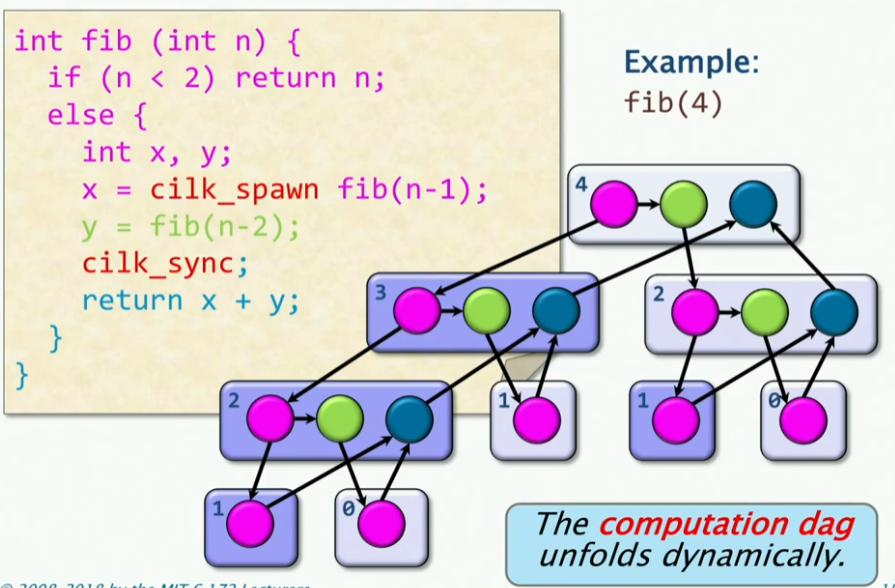
image-20240522203602936

这样就引入了一张图，我们称为Computation Dag，这样的图可以很好的表示出并行性。我们定义如下：

一个并行的指令流是一个Computation Dag，也就是 G = (V, E). 这是一个有向无环图，其中每个节点代表一个指令，每个边代表一个依赖关系。如果一个节点的所有父节点都已经执行完毕，那么这个节点就可以执行。

  • DAG图中每一个顶点对应于一条Strand，其是一个指令序列， Strand内部是串行的，Strand之间是并行的
  • DAG图中的边，我们有spawn edges、call edges、return edges、continue edges
    • spawn edges：表示一个strand的开始
    • call edges：表示一个转到调用函数的边上
    • return edges：表示一个strand的返回
    • continue edges：表示一个strand的继续
  • 并行循环(cilk_for)被转换为嵌套的spawns和syncs，使用的是分治递归的方法
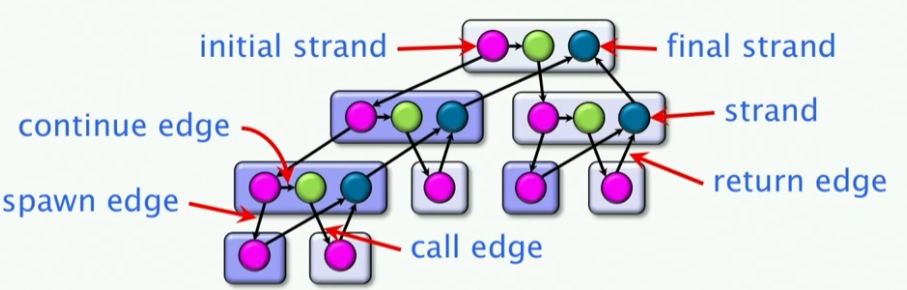
image-20240522205147557

我们假设上述图中每一个Strand，即链都是在一个单位时间执行完毕（不过现实中并不是这样，为了简单起见），那么这次计算的并行度是多少？

要回答上述的问题，我们首先得知道几个概念：

Amdahl’s law: 如果你的程序中有百分之50并行、百分之50串行，那么你的程序的加速比最多是2倍，不管你有多少核心。这句话很好理解，也就是说我百分之50的时间是在处理串行程序，如果我有无数的核心，串行程序的时间是不会变的，因此加速比最多是2倍。那么，推理到常规，如果程序中串行占比为$$\alpha$$，并行占比为$$1-\alpha$$，那么加速比为$$\frac{1}{\alpha + \frac{1-\alpha}{p}}$$，其中加速比的upper-bound是1α\frac{1}{\alpha}​。其中p为核心数。

我们来计算下图的计算并行性：

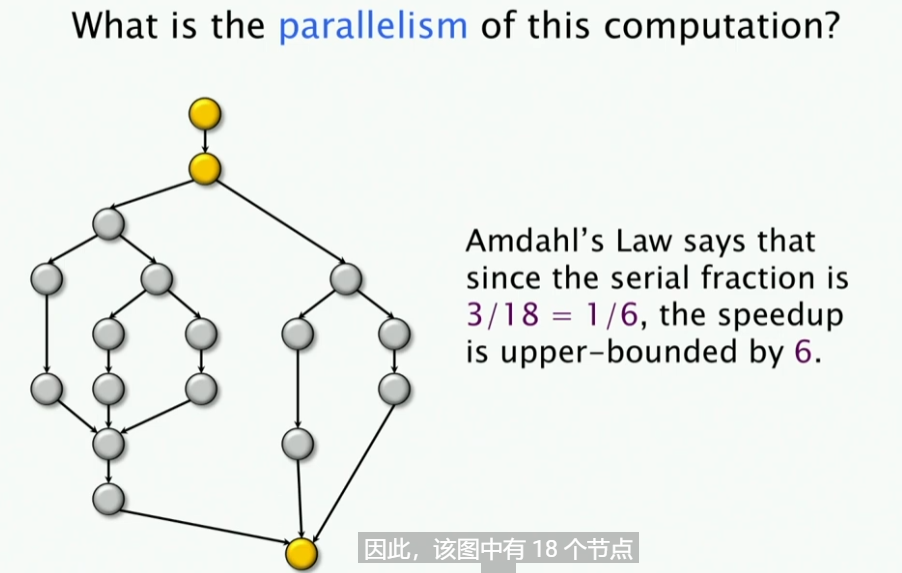
image-20240522211355048

我们来看，这里有多少串行的点，这里有三个串行的节点。（除了这三个节点之外，其它的节点均在并行的路线上）因此，我们知道，这个串行的比例是1/6，因此其加速比的上限是6倍。

但是实际上上面的定义较为宽松了，其在实际上并没有什么那么有用，因此我们更进一步：

  • 我们定义TPT_P为程序在P个处理器上面的执行时间，并且我们定义T1T_1为程序在一个处理器上面的执行时间，也就是工作时间，我们定义为work，即工作（比如上述节点一共有18个，因此我们定义work为18）
  • 我们定义T∞T_{\infty}为span，即跨度，跨度也称为图的关键路径长度或者计算深度。这个等于图中找到的最长有向路径（上图中的span即9）

然后，我们有两个公式：

  • TP≥T1/PT_P \geq T_1 / P Work Law
  • TP≥T∞T_P \geq T_{\infty} Span Law

上述两个公式都是显然的。

image-20240525164648661

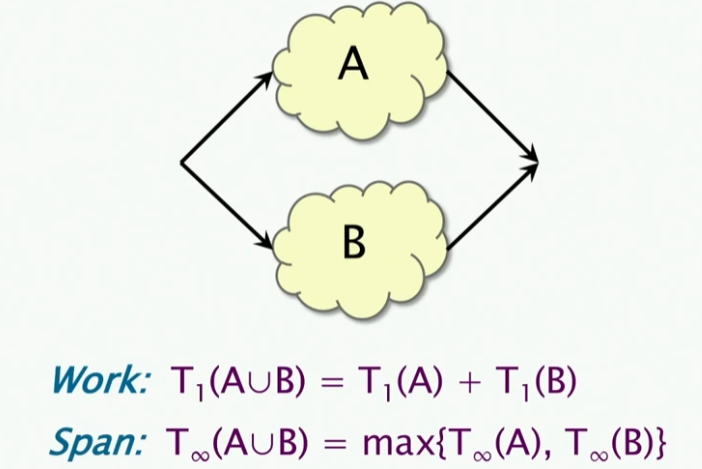
我们考虑串行的情况，不管是work还是span，A和B的联合都是其分开之和，这很好理解，因为我们要在B启动之前去启动A。而对于我们使用并行的情况下，其结论就不一样了：

  • work的联合不变，因为你还是有那么多的工作要去做
  • span的联合是取最大值，因为你要等待最长的那个时间
image-20240525165007994

我们定义在P个处理器上的speedup=T1/TPT_1/T_P，如果这个值小于P，说明得到的是亚线性的加速比，如果这个值大于P，说明得到的是超线性的加速比。这个值是不可能大于P的，因为我们有Amdahl’s law，因此我们的加速比的上限是P，即线性加速比。那么我们可以得到最大的可能的加速就是：T1/T∞T_1/T_{\infty}，所以上述图中，最大的计算比为2.

Quicksort Analysis

我们来看一个并行的快排的例子：

1
2
3
4
5
6
7
8
static void quicksort(int64_t *left, int64_t *right) {
    int64_t *p;
    if(left == right) return;
    p = partition(left, right); // 该函数的作用是随机选择一个主元，小于这个主元的放左边，大于的放右边，返回一个指向主元的指针
    cilk_spawn quicksort(left, p);
    quicksort(p+1, right);
    cilk_sync;
}

可以很清楚地看见，上述的左边部分排序和右边部分的排序是可以并行的。因此我们使用cilk_spawn来实现并行。

现在有一个问题，就是我们假设我们分类的数目是100万，那么这里的并行度是多少？

我们使用Cilkscale来绘制出并行度（加速比与处理器数量的关系图），这张图是通过单个处理器上面的运行时间除以P个处理器上面的运行时间得到的。这个就是实际观察得到的加速比。

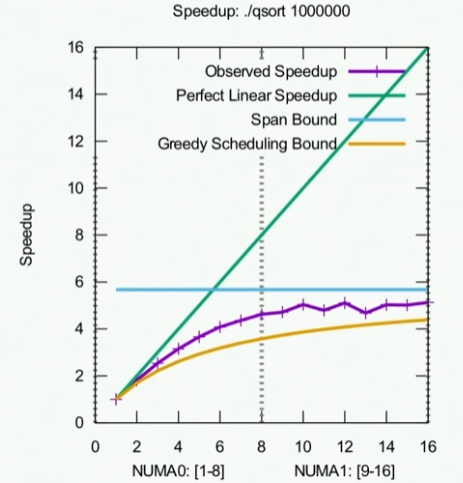
image-20240525190205588

我们很容易知道上述蓝色的图线表示Span Bound即在有无限多的处理器上面，最大的加速比会是多少。这里的结果大概接近6；对于绿色的线，是根据work law 得出的，其实就是一条斜率为1的直线，我们的观测结果要在这两条线的下面。

至于为什么我们观测的结果是锯齿状的，我想是因为噪声的影响

但是如果我们实际上去计算这个值，我们对于预期的并行度计算如下：

image-20240525192147351

实际上，上述计算还是有很多边界常数项的，我们只能说是Order of magnitude（数量级），但是我们可以看到，我们的实际观测值是符合预期的。

Scheduling Theory

不同的线程是如何映射到处理器的呢？我们来了解一下调度理论

Greedy Scheduling

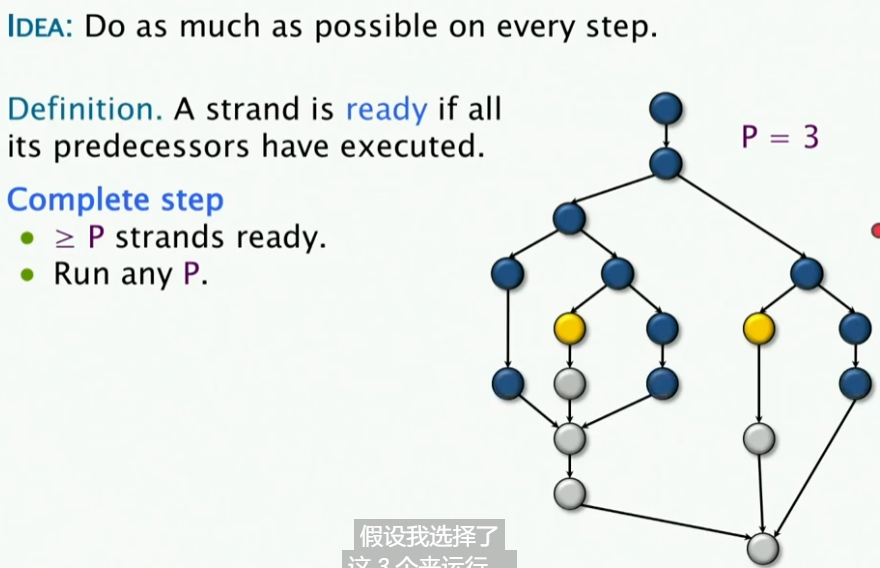
贪心调度的思想就是在每一步都尽量做更多的计算工作

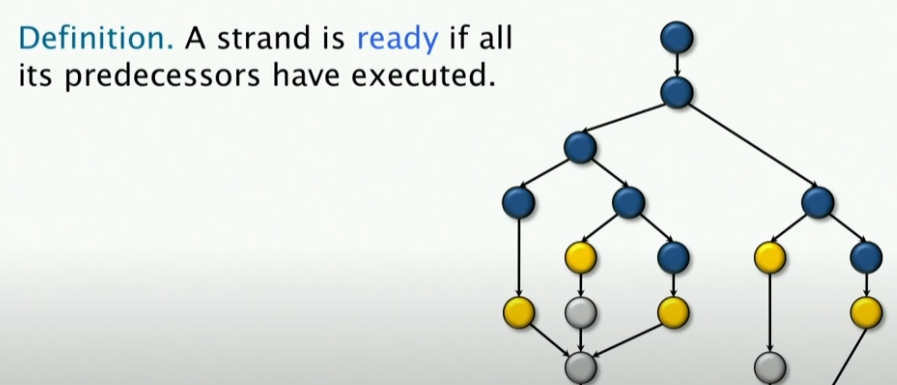
image-20240525193014317
  • 我们定义一个Strand为Ready状态当其所有的父节点都已经完成，这样的Strand就是Ready状态。
  • 我们定义Complete step即有 ≥P\geq{P}的Strand，我们就称为Complete step

那么，对于一个贪婪调度算法， 它会在一个Complete step怎么做呢？——比如说我这里的P=3，那么它就会选择任意三个Strand去执行。假设我让下面这三个节点去运行，事实证明，这样的结果是很差的，因为它们无法让任何新的Strand变为Ready状态。 😕

image-20240525193924547
  • 我们继续定义Incomplete step，即有 <P<P的Strand，我们就称为Incomplete step，也就是类似上图中的状态

所以说，如果我这里有两个Ready Strand，有三个处理器，我应该在Incomplete Step做什么呢？——那么我们就简单地Run all of them，因为我处理器有三个，而我只有两个Ready Strand，因此我就让这两个Ready Strand去运行。不需要竞争调度。 😕

然后，我们使用Complete Step和Incomplete Step去分析贪婪调度下的性能：

TP≤T1/P+T∞T_P \leq T_1/P +T_{\infty}

该公式的简单证明如下：

  1. 首先Complete Steps （针对有多少个这样的状态）不会超过 T1/PT_1/P，这是很显然的
  2. 然后Incomplete Steps不会超过T∞T_{\infty}，这也是显然的，因为如果我们执行了一次Incomplete Steps，那么这个图(DAG)的最长路径就会减少一个节点，因此不会超过T∞T_{\infty}

因此，我们可以得到上述的公式。正好是两个边界之和。

Optimality of Greedy

对于上述公式有一个推断，就是任何的贪婪调度都能在两倍之内的最优调度时间内（Optimal Running time）实现。

（所谓Optimal Running time，即知道一切未来情况，分析得到的最优解）

由之前的这两个Laws，我们可以得到下述结论：

  • TP≥T1/PT_P \geq T_1 / P Work Law
  • TP≥T∞T_P \geq T_{\infty}​ Span Law

TP∗≥max⁡{T1/P,T∞}T_P^{*}\geq\max\{T_1/P,T_{\infty}\}，在这个公式中，$$T_P^{*}$$是最优调度时间，即Optimal Running time。

因此我们就有：

TP≤T1/P+T∞T_P\le T_1/P+T_{\infty}

TP≤2⋅max⁡{T1/P,T∞}T_P \le 2\cdot \max \left\{ T_1/P,T_{\infty} \right\}

TP≤2⋅TP∗T_P\le 2\cdot T_{P}^{*}

Linear Speedup

另一个关于贪婪的推论是，如果当T1/Tinfty≫PT_1/T_{infty}\gg{P}，那么这个贪婪调度将会得到接近线性的加速比。

image-20240525201155439

后面的课程将会更加偏向于算法，下一节将会涉及分治递归，希望我准备好了 😇 😇