性能优化学习笔记3

Class3——Bit Hacks(位操作魔法)

在国外计算机课程中，word是一个抽象的概念，不应该直接视为4字节，8字节，16字节等。在这里，我们把word视为一个抽象的概念，它可以是任何长度的二进制数，我们可以通过位操作去实现一些有趣的操作。

无符号整数以及有符号整数的二进制表示

首先我们进行知识点回顾：

原码：将一个整数，转换成二进制，就是其原码。如单字节的5的原码为：0000 0101；-5的原码为1000 0101。

反码：正数的反码就是其原码；负数的反码是将原码中，除符号位以外，每一位取反。如单字节的5的反码为：0000 0101；-5的反码为1111 1010。

补码：正数的补码就是其原码；负数的反码+1就是补码。如单字节的5的补码为：0000 0101；-5的原码为1111 1011。

补码的计算公式如下：

$$x=(\sum_{k=0}^{w-2}x_k2^k)-x_{w-1}2^{w-1}$$

其中，$x_{w-1}$为符号位，$x_k$为二进制位。

所以我们就有一个通用的公式：

$$x+\sim{x}=-1$$

也就是原码加上其反码等于-1

然而计算机中的数，并没有人为定义的那么多表示，我们只有补码的表示，因此，我们说，这里的x本身就是补码，而$\sim{x}$代表的是按位取反的操作，它是一种操作，在英文表达里面我们叫做ones’ complement，也就是取反。

那么我们把等式移动一下：

$$-x=\sim{x}+1$$

这就是我们常说的负数的补码的计算方法。

实际上，对于二进制操作，我们的算术表达式有以下几种：

operator	Description
&	AND
|	OR
^	XOR
$\sim$	NOT （按位取反）
<<	shift left
>>	shift right

接下来就是正式的问题叙述了。

设置第K位的比特值（set the kth Bit）

其核心思想就是 Shift and OR，这两个操作在顶层架构设计上都是基本的操作。

$$y=x|(1<<k)$$

清理第K位的比特值

思想为 Shift, completement, and AND

$$y=x\&\sim(1<<k)$$

第K位实现翻转

Shift and XOR : y = x ^ (1<<k)

在我们处理编码数据的时候，对某个word x 的某个比特区域进行提取

我们的思想就是 Mask and shift

$$y=(x \& mask) >> shift$$

Example：

数据	值
x	1011110101101101
mask	0000011110000000
x&mask	0000010100000000
x&mask>>shift	0000000000001010

特别在于C语言中的位字段功能，汇编器就会为你进行这样的操作。

对某个比特区域设定值

思想：翻转mask去让该区域成为0，然后进行OR操作

$$x=(x\& \sim mask)|(y<<shift)$$

Example： shitf=7

数据	值
x	1011110101101101
y	0000000000000011
mask	0000011110000000
x&～mask	1011100001101101
x = (x&～mask)|(y<<shift)	1011100111101101

实现no temp swap（交换x与y）

我们可以通过位操作去交换x和y并且不带来任何的临时数据

三次异或操作：

x = x ^ y;
y = x ^ y;
x = x ^ y;

这个实现的思想很简单，其实就是利用了异或的性质，我们可以通过异或的性质去实现交换。

也就是我们可以看到，实际上最后是y=x ^ y ^ y=x，x = x ^ y ^ x ^ y ^ y = y所以我们可以实现交换。

1. 我们再实际上去看这个思想，这个思想首先是为了创建一个mask，告诉你x和y的哪些位是不同的，不同的位置为1
2. 然后，第二行的意思就是，根据这个mask，对y做flip操作，这样就实现了把y变成x
3. 第三步，既然y变成了x，那么我对这个y继续做翻转，实际上就是对x做反转，赋值给了x，这样就实现了交换。

[!IMPORTANT]

注意，这样的swap操作在指令级的并行性能上面效果很差，因为这样的操作会引入数据的依赖性，所以在实际的代码中，我们不会使用这样的操作，而是使用临时变量去实现交换。意思就是，这三行代码有顺序依赖性。而如果我们引入临时变量，我们就可以实现同时对x和y进行赋值。

找到x和y的最小值的数

找到x和y中最小的数，把它存储到r中

一般的操作如下：

if(x<y)
    r=x;
else
    r=y;

## or
r = (x<y)?x:y;

上述两个操作是等价的。但是如果代码中存在分支，现代机器进行分支预测的时候，如果错误地预测了分支，那么就会引入pipeline的flush，这样会导致性能的下降。现代的编译器会尽量避免分支的操作。

那么我们如何通过位操作去实现无分支的操作呢？

r = y ^ ((x ^ y) & -(x < y))

这个操作无非就是分情况去思考，如果 x<y，C语言返回的是1，去负数，其补码表示全1，那么结果就变成了 r = y ^ (x ^ y) = x

那么如果x>=y，C语言返回的是0，去负数，其补码表示全0，那么结果就变成了 r = y ^ 0 = y

合并两个有序列表

一般的合并两个有序列表的思想如下：

static void merge(long * __restrict C,
                  long * __restrict A,
                  long * __restrict B,
                  size_t na,
                  size_t nb) {
    while(na > 0 && nb > 0) {
        if(*A < *B) {
            *C++ = *A++;
            na--;
        } else {
            *C++ = *B++;
            nb--;
        }
        while(na > 0) {
            *C++ = *A++;
            na--;
        }
        while(nb > 0) {
            *C++ = *B++;
            nb--;
        }
    }
   
## restrict关键字是告诉编译器，这是唯一的指向该数据的指针的，该数据被其他指针所引用，这样会让编译器进行更好的优化。

我们可以观察到，这里一共有四个分支，除了第二个分支（if-else）是不可预测的，其他三个分支（while）是可预测的。因为其他三个分支基本上除了最后一次之外，其都是要进行运行的。而对于第二个分支，编译器预先并不知道A和B的值，所以这个分支是不可预测的。

那么我们如何通过位操作去实现无分支的操作呢？

static void merge(long * __restrict C,
                  long * __restrict A,
                  long * __restrict B,
                  size_t na,
                  size_t nb) {
    while(na > 0 && nb > 0) {
        long cmp = (*A < *B);
        long min = *B ^ ((*A ^ *B) & -cmp);
        *C++ = min;
        A += cmp; na -= cmp;
        B += !cmp; nb -= !cmp;
    }
    while(na > 0) {
        *C++ = *A++;
        na--;
    }
    while(nb > 0) {
        *C++ = *B++;
        nb--;
    }
}

[!IMPORTANT]

同样要注意的是，在现代机器上，使用这种无分支的操作，可能会引入更多的指令，因为这种操作会引入更多的位操作，所以在实际的代码中，我们不会使用这样的操作，而是使用分支操作。（因为现代编译器足够聪明，比如Clang，其内部实现了无分支比较），所以这个tirck不好用

那么，既然这些Bit Tricks不好用，那么我们为什么要学习呢？

1. 因为这些是编译器干的活，这帮助我们理解编译器的工作原理，至少不会在看汇编代码的时候一脸懵逼
2. 有时候，我们需要在没有编译器的情况下，进行一些位操作，比如在嵌入式系统中，我们需要对硬件进行操作，这时候就需要我们自己去写位操作的代码
3. 有的时候编译器并不会帮我们做这些优化，我们需要自己去做这些优化，这时候就需要我们自己去写位操作的代码
4. 这些技巧可以扩展在vectorization，parallelization，和其他的优化上面，这些技巧是我们学习更高级优化的基础
5. 这很有趣 🤣

Modular Addition(模加法)

我们去计算 (x+y) mod n，我们假设 0<=x<n and 0<=y<n

因此，计算公式为： r = (x+y) % n;

我们都知道， 除法是有代价的，除非它是2的幂次方（如果是2的幂次方，我们就直接做right shift操作），否则我们都不会使用除法，因为除法是很慢的。

有一种不使用除法的方法：

z = x + y;
r = (z < n) ? z : z - n;

这样，就会带来分支预测的不准确性，我们可以引入位操作去实现无分支的操作：

z = x + y;
r = z - (n & -(z >= n));

Round-up to a power of 2(向上取2的幂次方)

计算： $$2^{\lceil log_2(n) \rceil}$$

计算代码如下：

uin64_t n;
--n;
n |= n >> 1;
n |= n >> 2;
n |= n >> 4;
n |= n >> 8;
n |= n >> 16;
n |= n >> 32;
++n;

这里举例子：

n	Action
0010000001010000	——
0010000001001111	–n
0011000001101111	n |= n >> 1
0011110001111111	n |= n >> 2
0011111111111111	n |= n >> 4
0011111111111111	n |= n >> 8
0011111111111111	n |= n >> 16
0011111111111111	n |= n >> 32
0100000000000000	++n

实际上，核心思想把n的最高位的1后面的所有位都变成1，主要是通过右移动操作来实现的。我们把这个填充动作称为Populate，而我们把population指代二进制数中1的个数

而为什么我们需要首先对n进行减1操作呢？因为这是防止出现n本身就是2的幂次方的情况，这样的话，如果不减1，那么操作就错误。

为什么这里是最后进行32次移位呢？因为我们假设n是64位的，所以我们需要进行32次移位。这是根据Populate的性质决定的。

Least Significant Bit（最低有效位）

我们要计算一个word x中最低有效位1相对应的掩码，这个掩码指示了最低有效位1的位置。

r = x & -x;

我们来看看它为什么会起作用：

Example	Value
x	001000001010000
-x	110111110110000
x & (-x)	000000000010000

核心思想就在于：-x = ~x + 1，这个操作实际上就是把x的最低有效位1保留下来，其他的位置都变成了0。

那么下一个问题就在于，得到了这个掩码，我知道它现在是2的次幂，我应该如何去计算这个最低有效位1的位置呢？

Log Base 2 of a Power of 2（2的幂次方的对数）

也就是计算$$\log_2(x)$$，其中x是2的幂次方。

const uint64_t deBruijn64 = 0x022fdd63cc95386d;
const convert[64] = {
    0, 1, 2, 7, 3, 13, 8, 19, 4, 25, 14, 28, 9, 34, 20, 40,
    5, 17, 26, 38, 15, 46, 29, 48, 10, 31, 35, 54, 21, 50, 41, 57,
    63, 6, 12, 18, 24, 27, 33, 39, 16, 37, 45, 47, 30, 53, 49, 56,
    62, 11, 23, 32, 36, 44, 52, 55, 61, 22, 43, 51, 60, 42, 59, 58
};

r = convert[(x * deBruijn64) >> 58];

这个方法就像魔术一样，实际上对于每一个不同长度的数，都有一个对应的deBruijin序列，这个序列是固定的，我们可以通过这个序列去计算2的幂次方的对数。也就是说，如果我的序列为8位，那么deBruijin也是8位，我们可以通过这个序列去计算2的幂次方的对数。

但是这个方法受到乘法和查表性能的限制，这样的代价很大，实际上，现在已经有一个硬件指令可以直接计算2的幂次方的对数，这个指令是BSR（Bit Scan Reverse），这个指令可以直接计算2的幂次方的对数。（从最高位开始扫描，找到的是最高位的1的位置）

N皇后问题

N皇后问题是一个经典的问题，我们要在一个N*N的棋盘上放置N个皇后，使得每个皇后都不在同一行，同一列，同一对角线上。并计算出所有的解。

最常见的解决N皇后问题的方法是回溯的方法，我们尝试逐行放置皇后，那么对于每一行要解决的就是皇后在该行的位置，然后，如果我们不能在任何一行放置皇后，那么我们就回溯到上一行，重新放置皇后。

好的，要想解决这个问题，我们首先从棋盘的表示开始入手，棋盘的表示可以如下：

1. 二维数组， N*N bytes
2. N*N bits
3. N bytes(这里不一定是Bytes，因为可能不止8位皇后)
4. 3 bitvectors of size n, 2n-1, 2n-1

使用位向量的方法，我们可以很容易的实现对于行，列，对角线的检查，我们可以通过位操作去实现这个检查。

首先我们有一个down，left，right的位向量，down表示当前列是否有皇后，left表示左对角线是否有皇后，right表示右对角线是否有皇后。

所以要进行三次检测，对应的表达式如下：

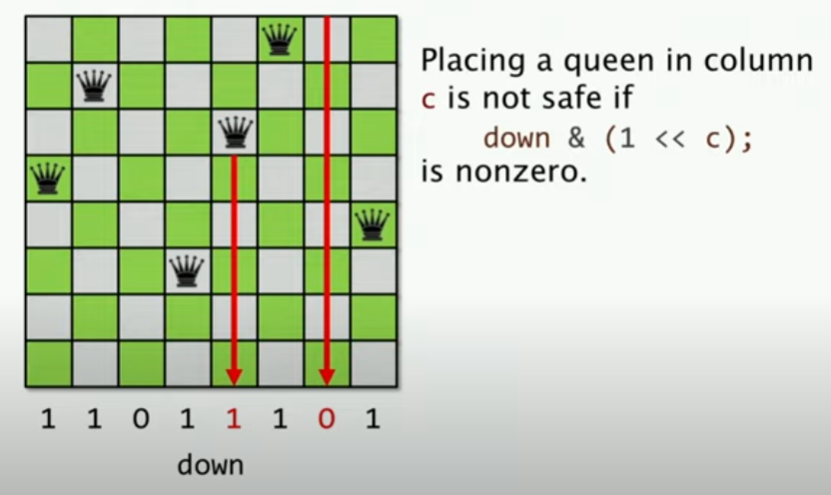
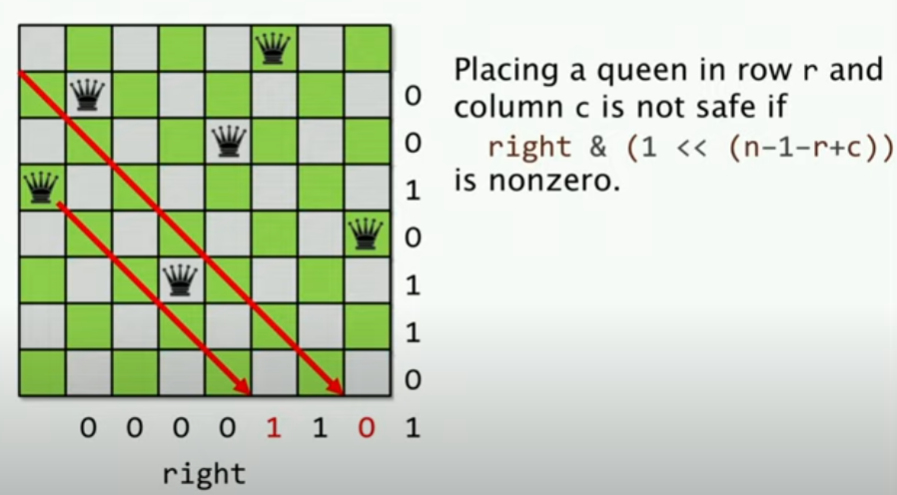
我们假设r为放置的行，c为放置的列的位置。

首先检测是否在同一列：

down & (1 << c) 如果非0，就表示当前行已经有皇后了

然后我们分别检测左对角线和右对角线：

left & (1 << (r+c)) 如果非0，表示当前朝向左下的对角线已经右皇后了

right & (1 << (n-1-r+c)) 如果非0，表示当前朝向右下的对角线已经右皇后了

Count the number of 1 bits in a word x: simplest solution

简单的方法就是不断去消除最小有效位1

for(r=0; x!=0; ++r)
    x &= x - 1;

实际上上述减1的操作，就是在最小有效位以及最小有效位的后面所有位实现反转，再与本身进行按位与操作，就消除了最低有效位的1，这样循环得出的结果r就是其所有1的数目

这样做的问题在于，如果这个数很大， 并且位数很多，那么这个迭代的运行时间就会很长很长。

我们的另一个方法就是使用look-up table：

static const int count[256] = 
{0,1,1,2,1,2,2,3,1,...,8};

for(r=0; x!=0; x>>8)
    r += count[x & 0xFF];

这种方法的性能会受到x的大小影响，其瓶颈在于内存操作的代价，因为这个表存在内存中的，每次都要访存。

实际上，我们可以把这些数据存在registers上面，同样的，和第一节课一样的思想，做并行的分治合并操作：

Parallel divide-and-conquer：

//create masks
M5 = ~((-1) << 32); // 0^32 1^32 (表示高位有32个0 低位是32个1)
M4 = M5 ^ (M5 << 16); // (0^16 1^16)^2 两组这样的数
M3 = M4 ^ (M4 << 8);// (0^8 1^8)^4 四组这样的数
M2 = M3 ^ (M3 << 4);// (0^4 1^4)^8 八组这样的数
M1 = M2 ^ (M2 << 2);// (0^2 1^2)^16 十六组这样的数
M0 = M1 ^ (M1 << 1);// (01)^32 三十二组这样的数

// compute popcount
x = ((x>>1) & M0) + (x & M0);
x = ((x>>2) & M1) + (x & M1);
x = ((x>>4) + x) & M2;
x = ((x>>8) + x) & M3;
x = ((x>>16) + x) & M4;
x = ((x>>32) + x) & M5;

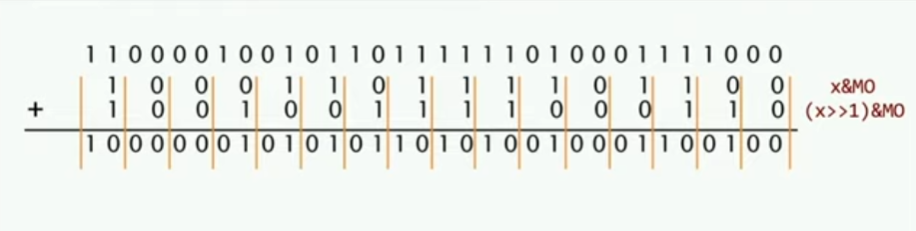
第一个式子的意思告诉我们，每两组有多少1，第一次计算分别是得到偶数和奇数位置下的数值，然后对齐，计算即可，这一次计算实际上是两个操作，可以并行。吊炸天！！！ 🥵

第二次操作：

第二次操作的意义实际上就在于把第一次操作得到的结果再分组，再对齐，这样相加完成之后，得到的就是每四组有多少个1

我们可以对比原始的x数据，可以看到，每四个一组，对应的计数结果都是正确的！

后面的操作一模一样，最后我们得到

这样的话，我们实现的方法复杂度只有 O(lgw)（以2为底）的复杂度，其中w为这个word的长度。

需要注意的是，一开始x的值由于不分组的原因，如果计算x的时候表达式写成类似”x = ((x>>4) + x) & M2;“这样的形式，很有可能出现溢出，但是随着后面的分组，就不必担心溢出问题，所以才看见代码中两种计算方法的不同之处，而且我们可以知道：按位与运算是符合交换律的！ 😎

因此，我们看到的是，我们对于后面的四次运算，都是作为一条指令去计算的，并不需要做两次的AND运算

[!IMPORTANT]

还是那句话，现在大部分的机器都是支持做popcount的（population count），而且运算速度比你以任何方式写出来的代码都要快！

练习：如何根据这个内置的popcount去计算一个2的次幂的数到底是2的几次幂？

对这个数减去1，然后用popcount即可！