Class1——Matrix Multiplication

写在前面：

首先第一次听到性能优化是在我一个朋友推荐下😐，认识了一位在小红书工作的学长，当时莽撞得问他：我想做您这个方向(其实就是想找个实习丰富自己的简历)，但是龙哥(我们称这位大神叫龙哥，想加入他就加入龙门)直接问我：你为什么要做这个方向呢？你有没有分布计算的经历？————显而易见，我是没有这个经历的，他也委婉得拒绝了那个莽撞的我，并跟我说，不管你以后做不做这个方向，学习这些都是有用的，我看了第一节课，感觉蛮有兴趣，于是关于这个主题的笔记就开始了。

这个文章的核心思想就是：

If programmers are so willing to sacrifice performance for these properties, why study performance?

Cause performance is the currency of computing !

直到近期，英伟达发布了自己的最新架构Blackwell，B200 芯片，我们才认识到，原来他的眼光并没有停留在AI方向，而是跑向了各种赛道，去为各个方向或者新的交叉方向提供算力，以后英伟达即算力，把自己的产品深深绑定，可见其眼光的独到。

因此，我认为作为一个计算机社畜，有必要系统学习一下performance engineering ，不管是从软件层面还是底层架构(虽然我也不知道我能坚持多久😟，所以还是尽早开始写，说不定某个将来性能优化成为国内必修课的时候，有些人能看到我的文章😳)

摩尔定律的失效

在2024年之前，基本上都是半导体技术产生的巨大进步从而为计算机行业造成贡献，因此那个时候的摩尔定律和时钟频率缩放本质上都性能货币(performance currency)的印刷机，我们只需要让硬件做得更快就行了！

但是当时钟频率趋于稳定应该怎么办呢？(如果时钟频率继续往上升，晶体管密度就上升，功耗就会不断增加，如果单芯片晶体管还是成倍增加，那么会受到物理极限，超温，量子方面的不稳定性影响)

也许在不久的将来，会开发出新的半导体材料，但是并行计算、性能优化仍然大有可为，这不得不学了☹️

因此，这些芯片公司在04年之后，开始着眼于多核，可惜多核虽然好，但是使用这种神秘的力量并不是免费的，我们需要掌握并行编程，好的，接下来就根据一个又一个研究课题来学习性能优化。

Matrix Multiplication

对于一个矩阵：

$\left[ \begin{matrix} c_{11}& c_{12}& \cdots& c_{1n}\\ c_{21}& c_{22}& \cdots& c_{2n}\\ \vdots& \vdots& \ddots& \vdots\\ c_{n1}& c_{n2}& \cdots& c_{nn}\\ \end{matrix} \right] \ =\ \left[ \begin{matrix} a_{11}& a_{12}& \cdots& a_{1n}\\ a_{21}& a_{22}& \cdots& a_{2n}\\ \vdots& \vdots& \ddots& \vdots\\ a_{n1}& a_{n2}& \cdots& a_{nn}\\ \end{matrix} \right] \ \cdot \ \left[ \begin{matrix} b_{11}& b_{12}& \cdots& b_{1n}\\ b_{21}& b_{22}& \cdots& b_{2n}\\ \vdots& \vdots& \ddots& \vdots\\ b_{n1}& b_{n2}& \cdots& b_{nn}\\ \end{matrix} \right]$

$c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj}$

如果单纯对于改矩阵进行运算，那么运算次数就是 $ 2n^3 $ 的计算次数，为了简单起见，我们假设，n 是 2 的精确幂，即： $n=2^k$

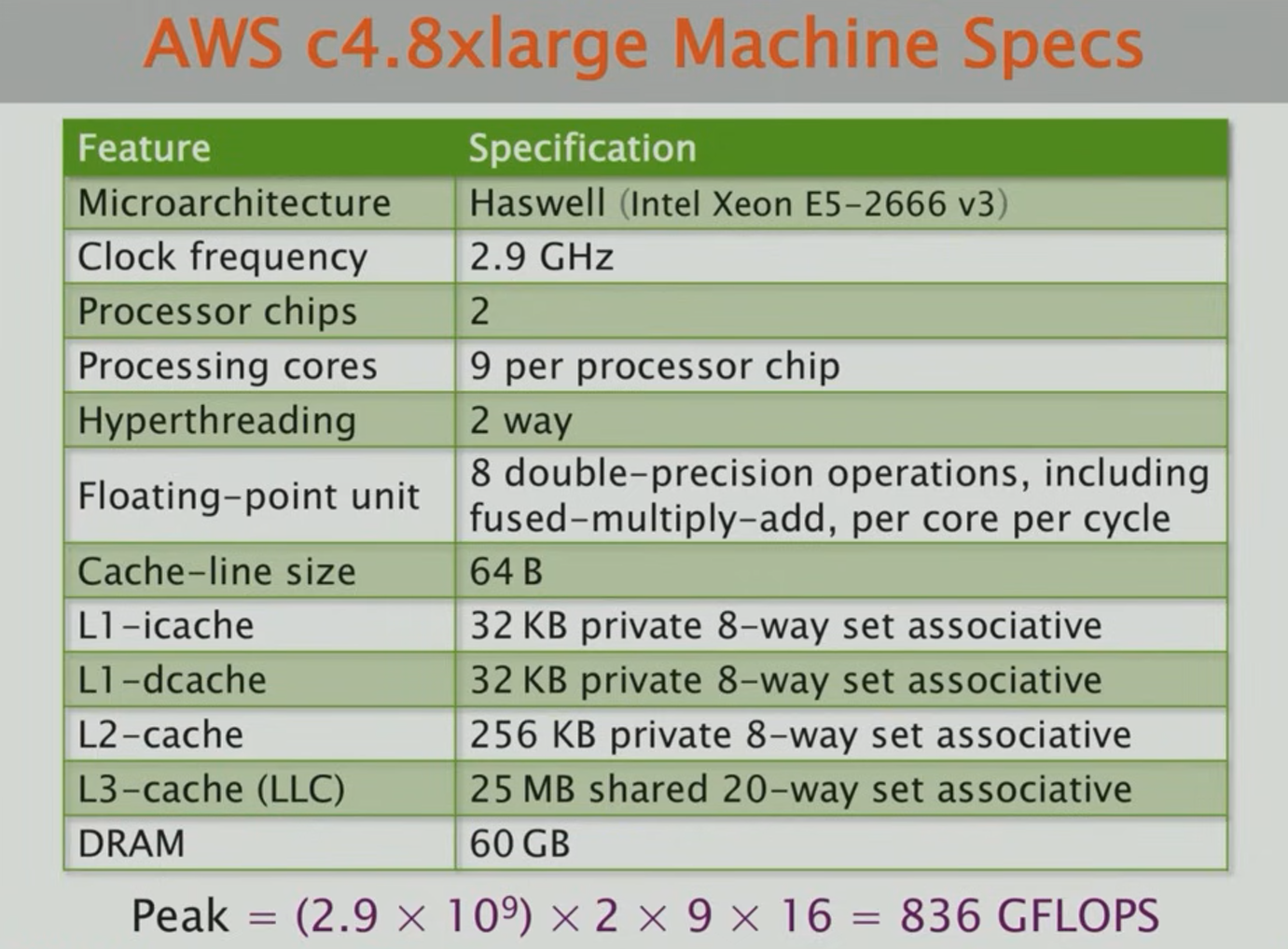
这里是某个e5神教的CPU，这里是某个计算性能的计算机，根据表中数据可以计算出对应的FLOPS参数，可见其峰值为 836GFLOPS

好的，现在我不使用python的专用矩阵运算库，我使用如下的代码：

import sys, random
from time import *

n=4096
A = [[random.random() 
     for row in range(n)] 
     for col in range(n)]

B= [[random.random()
    for row in range(n)]
    for col in range(n)]

C=[[0 for row in range(n)]
   for col in range(n)]

start = time()
for i in range(n):
    for j in range(n):
        for k in range(n):
            C[i][j]+= A[i][k] * B[k][j]
end = time()

print ('%0.6f'%(end-start))

这台e5神教机器跑出来的实验结果是：21042 seconds ≈ 6 h，现在我们来计算一下它的运算量去评估一下：

$Calculations = 2n^3 = 2(2^{12})^3=2^{37}$

可知，一共要做 $2^{37}$ 次数的浮点数运算，对应了FLOPS为：

$2^{37} / 21042 \approx 6.25\ MFLOPS$

$Peak \approx 836 \ GFLOPS$

python的运算时间约等于峰值的0.00075% ！！！！！！！！！！

接下来我们用不同的语言去写，做同样的事情，不改变循环体结构，那么这里时间对比如下：

Version	Implementation	Running time(s)	Speed up	GFLOPS	Percent of peak
1	Python	21041.67	1	0.007	0.001
2	Java	2387.32	9	0.058	0.007
3	C	1155.77	18	0.119	0.014

因为C是直接被编译成机器码，而Python是被解释的，在python执行一些指令比如乘法或者加法的时候，它不止在做乘法和加法，它还在试图先去理解你写的代码，因此python这种被解释的代码就是用性能货币去换编码简便性这一典型例子(所谓高级编程，在牺牲性能的前提下，支持动态代码更改等等操作)。

下图就是python在运行的时候解释器的状态

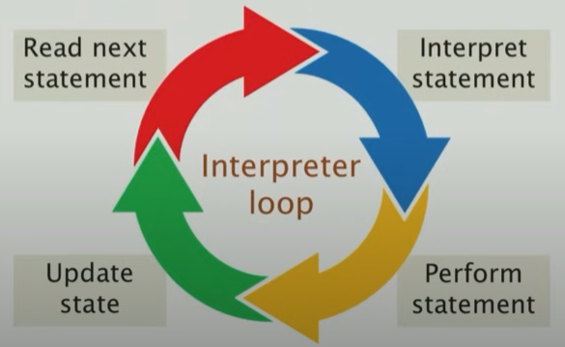
优化代码结构

我们可以改变循环的顺序，并且不影响其结果的正确性，现在我们的代码是 i、j、k三层嵌套的循环，那么这里我们可以改变一下代码顺序：

##origin
for(inti=0;i<n; ++i){
    for(int j=0;j<n; ++j){
        for(int k=0;k< n; ++k){
            C[i][j] += A[i][k] * B[k][j];
            
## change order version1
for(inti=0;i<n; ++i){
    for(int k=0;k<n; ++k){
        for(int j=0;j< n; ++j){
            C[i][j] += A[i][k] * B[k][j];
        
## change order version2
for(intk=0;k<n; ++k){
    for(int j=0;j<n; ++j){
        for(int i=0;i< n; ++i){
            C[i][j] += A[i][k] * B[k][j];

仅仅是循环的顺序改变，并不会改变循环的遍历结果，这样会对性能有影响吗？

结果就是，仅仅去改变循环顺序，就可以对running time 的影响造成18倍之多

Loop Order(outer to inter)	Running time (s)
i,j,k	1155.77
i,k,j	177.68
j,i,k	1080.61
j,k,i	3056.63
k,i,j	179.21
k,j,i	3032.82

所以为什么会发生如此大的影响？ 😐

Cache Localities

我们考虑矩阵在计算机内存中的存储结构：

矩阵是按照行的优先顺序排列在内存中，因此矩阵是根据内存的线性布局，也就是把row1、row2、row3线性展开如上图在memory中的表示。那么，对于不同的循环顺序，其in-memory访问下的locality如下所示：

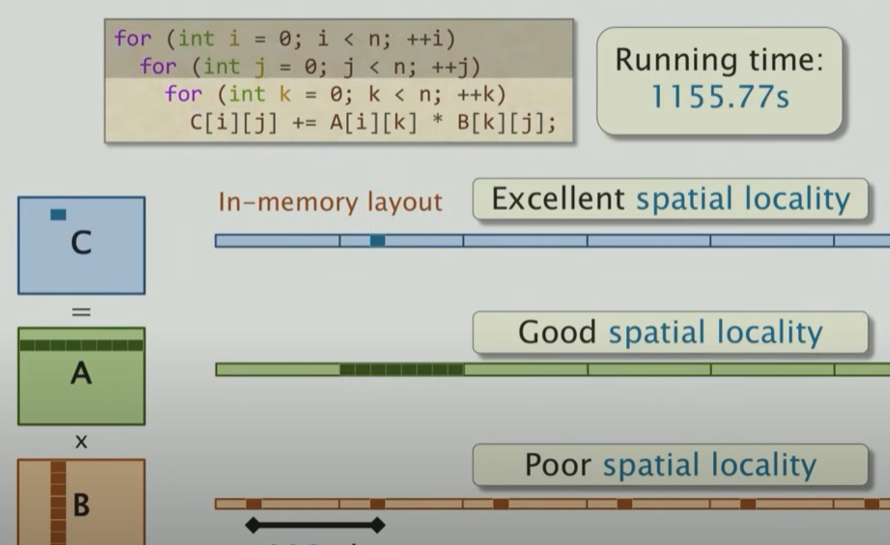
对于这种循环顺序，可知B的局部性很差，因此访问时间比较长，cache命中率很低，因此访问时间就长了，而对于下图这种顺序，效果就很好

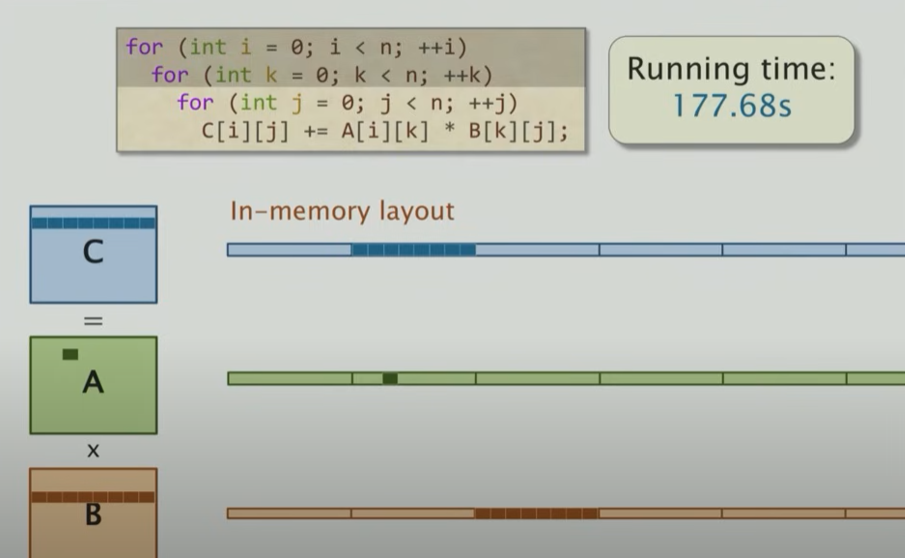
好的，现在我们的表格得更新一下，可以看见，提升很大，但是距离到达峰值还是很遥远！💀

Version	Implementation	Running time(s)	Speed up	GFLOPS	Percent of peak
1	Python	21041.67	1	0.007	0.001
2	Java	2387.32	9	0.058	0.007
3	C	1155.77	18	0.119	0.014
4	+ interchange loops	177.68	118	0.774	0.093

Change the compiler Flag

如果你对于编译器有一些了解，比如Clang的编译器，它提供了一组优化的开关，在编译的时候指定 -o 后面接数字即可，如下图所示

Multicore Parallelism

到目前为止，我们写的代码都是在一个CPU核心上面跑的，但是之前的表格上面写道：我们这台e5神机上面有18个核心，我们并没有完全使用！现在我们使用Cilk 这个轻量级并行编程框架，那么我们改写代码如下所示：

cilk_for(inti=0;i<n; ++i)
	for(intk=0;k<n;++k)
    	cilk_for(int j=0;j< n; ++j)
        	C[i][j]+= A[i][k]* B[k][j];

一般的cilk_for这个指令用在外部循环比较多，而且在这种情况下，不能使用内部循环的并行，也就是第二层循环的并行是不可取的。也就是说，这里针对当前循环顺序，只有三种并行方法：

针对 i 做cilk_for

针对 j 做cilk_for

针对 i、j 做cilk_for

那么为什么我只针对 k 做并行不可以？以下是回答：

数据依赖性：在矩阵乘法中，每次迭代C[i][j]的更新依赖于所有k的迭代结果的累加。使用cilk_for来并行化k循环可能会引入数据竞争，因为多个线程可能会同时尝试读写同一个C[i][j]元素。这违反了并行计算中一个重要的原则，即并行任务之间应该是相互独立的，不应有数据依赖关系影响它们的执行顺序。
并行开销：即便能够在技术上通过某种同步机制解决数据竞争问题（例如，使用原子操作或分别累加后合并结果），k循环的并行化可能带来的同步和管理开销也可能抵消因并行而获得的性能提升。并行计算的最大收益通常来源于能够独立完成的大块工作，而非大量细小的、需要频繁同步的任务。

同时，我们看是否使用方法3效果要比方法1好？

很明显，仅仅优化i效果是最好的，这涉及到操作系统的调度开销，因此我们有了这个对于循环并行优化的法则：

Rule of Thumb: Parallelize outer loops rather than inner loops

到目前为止，我们的优化表更新如下：

Version	Implementation	Running time(s)	Speed up	GFLOPS	Percent of peak
1	Python	21041.67	1	0.007	0.001
2	Java	2387.32	9	0.058	0.007
3	C	1155.77	18	0.119	0.014
4	+ interchange loops	177.68	118	0.774	0.093
5	+ optimization flags	54.63	385	2.516	0.301
6	Parallel loops	3.04	6921	45.211	5.408

这里可以观察到，使用并行优化之后，达到了近似18倍的加速，很明显使得所有的核心都被充分使用，但是并不是所有的代码并行优化都像循环这样简单！😡

Manage Cache Miss(Memory Access)

可以从上面的表看见，尽管我们做了如此多的优化，我们仅仅只是达到了peak的百分之5左右，很小很小，那么我们除了在编译、调度、代码这些方面做优化，我们还能在哪些方面优化？我们可以对于缓存命中做一些管理

例如如果我计算C的一行，我需要访问A的一行还有B的所有，那么需要上述的访问次数，很大，接近1700万次的内存访问！那么，如果我不是这样一行一行去计算，而是我使用block的概念去计算会发生什么呢？

我们每次使用64*64的block去计算，那么结果如下：

这样，只需要50万次的访存！很神奇，学到这里感觉很多东西都是相通的，甚至后面的课程里面有算法优化，引入了shortcut的概念，让我立马想到了resnet😕。这个缓存管理告诉了我们，如果我们的block设计更适合Cache的话，会使得速度快很多！

上述的这种方法其对应代码如下，其核心就是分解成多重的64*64矩阵，并在这个维度下面内嵌三层的loop

## Tiled Matrix
cilk_for(int ih=0;ih<n; ih += s)
	cilk_for(int jh=0;jh<n; jh += s)
    	for(int kh=0;kh<n;kh += s)
        	for(int il=0;il<s; ++il)
            	for(int kl=0;kl<s; ++kl)
                	for(int jl=0;jl<s; ++jl)
                    	C[ih+il][jh+jl] += A[ih+il][kh+kl]* B[kh+kl][jh+j1l];

这段代码的精华在于内三层的loop在顺序最优的情况下保持步长范围相等，也就是都是基于 s 的步长范围，然后为了使得矩阵乘法符合规范，距离三层嵌套最近的是k，也就是保持了代码的正确性，并且在最外两层使用了cilk_for使用多线程并行

这里s就是步长范围，我们测试不同的s:[4,8,16,32,64,128]等等，得到如下结果：

Tile Size	Running Time (s)
4	6.74
8	2.76
16	2.49
32	1.74
64	2.33
128	2.13

后面我们还可以使用分治递归的思想去做这种block 的计算，并且计算机一般都是很多层Cache，这里不做赘述了。

同时现在的硬件支持向量化，也就是嵌入式学到的SIMD指令(Single instruction stream-Mutiple data stream)，支持编译器级别的向量化，这会使得性能更好：

我们更新表格：

Version	Implementation	Running time(s)	Speed up	GFLOPS	Percent of peak
1	Python	21041.67	1	0.007	0.001
2	Java	2387.32	9	0.058	0.007
3	C	1155.77	18	0.119	0.014
4	+ interchange loops	177.68	118	0.774	0.093
5	+ optimization flags	54.63	385	2.516	0.301
6	Parallel loops	3.04	6921	45.211	5.408
7	+ tiling	1.79	11772	76.782	9.184
8	Parallel divide-and-conquer	1.30	16197	105.722	12.646
9	+ compiler vectorization	0.70	30272	196.341	23.486

好的，到目前为止第一堂课就结束了，结束之前这位教授还说了如下的一句话：

Matrix multiplication is a good example, but we generally won’t see such magnitude of improvement in other cases

因此尽管cuda在矩阵运算上优化很大，我们在并行计算优化上面还有很多需要做的。😧😧😧😧